SpectralDNS#
The spectralDNS project revolves around implementing high-performance flow solvers in Python, which is a modern and very high-level programming language. The project is supported through several grants from King Abdullahs University of Science and Technology, granting access to some of the world’s largest supercomputers. The work has been presented at several conferences and as invited talks
11’th International Conference on Scientific Computing and Applications
International Conference on Computational Science and Engineering
I3MS Seminar Series of the Institute for Modeling and Simulation, 6 Nov 2017 RWTH AAchen University
Predictive Complex Computational Fluid Dynamics, KAUST, May 2017
MekIT’17 National Conference on computational Mechanics, Trondheim, May 2017
The spectralDNS project on github contains several repositories, each representing a smaller part of the overall project. The most important are presented beolw.
spectralDNS#
The spectralDNS repository is home to several different pseudo-spectral Navier-Stokes and MagnetoHydroDynamics solvers. Most solvers are for triply periodic domains. The simplest possible Navier-Stokes solver is described by [Mortensen and Langtangen, 2016], who show that a highly efficient solver can be created using no more than 100 lines of code, using nothing more than standard tools like Numpy and MPI for Python. The DNS solver has been tested for a transitional Taylor-Green vortex using a computational box of size \(2048^3\). Accuracy is, well, spectral, and in benchmark tests on the Shaheen II supercomputer at KAUST it has been found to scale well up to 64,000 cores. A state-of-the-art spectral channel flow solver that is making extensive use of shenfun, has been described by [Mortensen, 2017]. Turbulent flow at \(Re_{\tau}=2000\) is shown in the movie below.
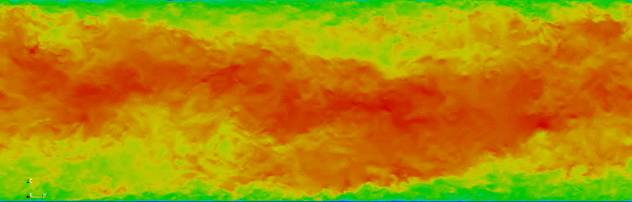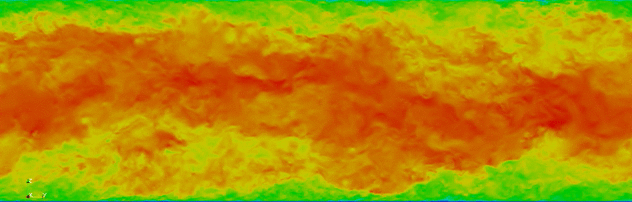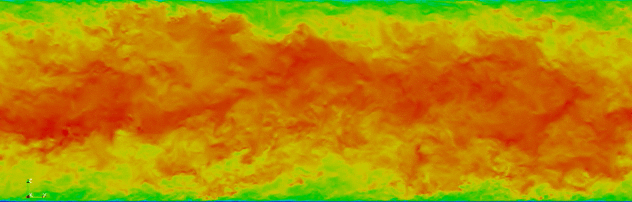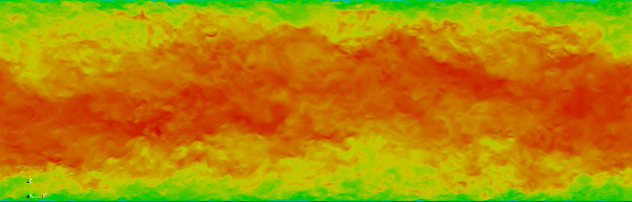
With colleagues at the Extreme Computing Research Center (ECRC), King Abdullah University of Science and Technology (KAUST), we have been using spectralDNS to investigate time integration of Fourier pseudospectral Direct Numerical Simulations [Ketcheson et al., 2020]. We investigate the use of higher‐order Runge‐Kutta pairs and automatic step size control based on local error estimation. We find that the fifth‐order accurate Runge‐Kutta pair of Bogacki and Shampine gives much greater accuracy at a significantly reduced computational cost.
Shenfun#
With the shenfun Python module [Mortensen, 2017] an effort is made towards automating the implementation of the spectral Galerkin method for simple tensor product domains, consisting of non-periodic and periodic directions. The user interface to shenfun is intentionally made very similar to FEniCS. Partial Differential Equations are represented through weak variational forms and solved using efficient direct solvers where available. MPI decomposition is achieved through the mpi4py-fft module, and all developed solvers may, with no additional effort, be run on supercomputers using thousands of processors.
An introduction to shenfun is given in [Mortensen, 2017], on readthedocs and the paper [Mortensen, 2018]. Shenfun is also used as PDE solver in the deep reinforcement learning paper by [Vignon et al., 2023] and to study the Rayleigh Taylor instability [Piterskaya et al., 2023]. Introduction to mpi4py-fftis given here and in [Dalcin et al., 2019, Mortensen et al., 2019]. Further documentation is found at
Try shenfun in the computational cell below. Modify to own liking and run interactively.
from sympy import symbols, cos, sin, pi
from shenfun import *
import matplotlib.pyplot as plt
%matplotlib inline
x, y = symbols("x,y")
C = FunctionSpace(50, 'Chebyshev')
F = FunctionSpace(50, 'Fourier', dtype='d')
T = TensorProductSpace(comm, (C, F))
u = project(sin(2*pi*x)*cos(pi*y), T)
X = T.local_mesh(True)
plt.contourf(X[0], X[1], u.backward(), 100)
plt.colorbar()
plt.show()
mpi4py-fft#
mpi4py-fft is a Python package for computing Fast Fourier Transforms (FFTs). Large arrays are distributed and communications are handled under the hood by MPI for Python (mpi4py). To distribute large arrays we are using a new and completely generic algorithm that allows for any index set of a multidimensional array to be distributed. We can distribute just one index (a slab decomposition), two index sets (pencil decomposition) or even more for higher-dimensional arrays.
mpi4py-fft comes with its own Python interface to the serial FFTW library. This interface can be used much like pyfftw, and even for real-to-real transforms, like discrete cosine or sine transforms. Further documentation is found at
Number of downloads from conda-forge:
References#
Lisandro Dalcin, Mikael Mortensen, and David E Keyes. Fast parallel multidimensional FFT using advanced MPI. Journal of Parallel and Distributed Computing, 2019. doi:10.1016/j.jpdc.2019.02.006.
David I. Ketcheson, Mikael Mortensen, Matteo Parsani, and Nathanael Schilling. More efficient time integration for fourier pseudospectral dns of incompressible turbulence. International Journal for Numerical Methods in Fluids, 92(2):79–93, 2020. doi:10.1002/fld.4773.
M. Mortensen. Shenfun - automating the spectral galerkin method. In In Bjørn Helge Skallerud and Helge Ingolf Andersson (ed.), MekIT'17 - Ninth national conference on Computational Mechanics. International Center for Numerical Methods in Engineering (CIMNE), 273–298. 2017. URL: https://arxiv.org/abs/1708.03188.
M. Mortensen and H. P. Langtangen. High performance Python for direct numerical simulations of turbulent flows. Computer Physics Communications, 203:53–65, 2016. doi:10.1016/j.cpc.2016.02.005.
Mikael Mortensen. A spectral-galerkin turbulent channel flow solver for large-scale simulations. arXiv preprint, 2017. URL: https://arxiv.org/abs/1701.03787.
Mikael Mortensen. Shenfun: high performance spectral galerkin computing platform. Journal of Open Source Software, 3(31):1071, 2018. doi:10.21105/joss.01071.
Mikael Mortensen, Lisandro Dalcin, and David Keyes. Mpi4py-fft: parallel fast fourier transforms with mpi for python. Journal of Open Source Software, 4(36):1340, 4 2019. doi:10.21105/joss.01340.
A. Piterskaya, W. J. Miloch, and M. Mortensen. A global spectral-Galerkin investigation of a Rayleigh–Taylor instability in plasma using an MHD–Boussinesq model. AIP Advances, 13(10):105319, 10 2023. doi:10.1063/5.0155976.
Colin Vignon, Jean Rabault, Joel Vasanth, Francisco Alcántara-Ávila, Mikael Mortensen, and Ricardo Vinuesa. Effective control of two-dimensional Rayleigh–Bénard convection: Invariant multi-agent reinforcement learning is all you need. Physics of Fluids, 35(6):065146, 06 2023. doi:10.1063/5.0153181.