Demo - Helmholtz equation on the unit sphere

Mikael Mortensen (email: mikaem@math.uio.no), Department of Mathematics, University of Oslo.

Date: April 20, 2020

Summary. This is a demonstration of how the Python module shenfun can be used to solve the Helmholtz equation on a unit sphere, using spherical coordinates. This demo is implemented in a single Python file sphere_helmholtz.py. If requested the solver will run in parallel using MPI.

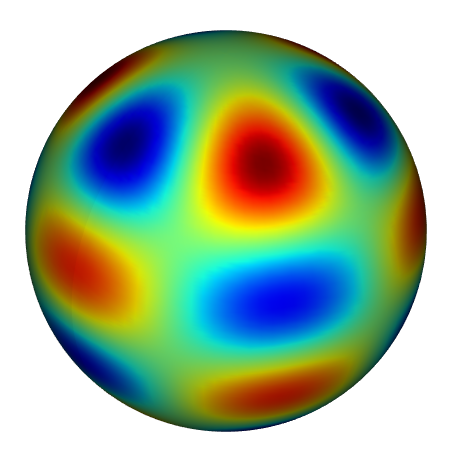
Figure 1: Helmholtz on the unit sphere.

Helmholtz equation

The Helmholtz equation is given as

\[ \begin{equation} -\nabla^2 u(\boldsymbol{x}) + \alpha u(\boldsymbol{x}) = f(\boldsymbol{x}) \quad \text{for }\, \boldsymbol{x} \in \Omega = \{(x, y, z): x^2+y^2+z^2 = 1\}, \label{eq:helmholtz} \tag{1} \end{equation} \]

where \(u(\boldsymbol{x})\) is the solution, \(f(\boldsymbol{x})\) is a function and \(\alpha\) a constant. We use spherical coordinates \((\theta, \phi)\), defined as

\[ \begin{equation} x = r \sin \theta \cos \phi , \label{_auto1} \tag{2} \end{equation} \]

\[ \begin{equation} y = r \sin \theta \sin \phi, \label{_auto2} \tag{3} \end{equation} \]

\[ \begin{equation} z = r \cos \theta \label{_auto3} \tag{4} \end{equation} \]

which (with \(r=1\)) leads to a 2D Cartesian product mesh \((\theta, \phi) \in (0, \pi) \times [0, 2\pi)\) suitable for numerical implementations. There are no boundary conditions on the problem under consideration. However, with the chosen Cartesian mesh, periodic boundary conditions are required for the \(\phi\)-direction. As such, the \(\phi\)-direction will use a Fourier basis \(\exp(\imath k \phi)\).

A regular Chebyshev or Legendre basis \(\psi_j(\theta) = \gamma_j(2\theta/\pi-1)\) will be used for the \(\theta\)-direction, where \(\gamma_j\) could be either the Chebyshev polynomial of first kind \(T_j\) or the Legendre polynomial \(L_j\). Note the mapping from real coordinates \(\theta\) to computational coordinates in domain \([-1, 1]\).

The spherical basis functions are as such

\[ v_{jk}(\theta, \phi) = \psi_j(\theta) \exp(\imath k \phi), \]

and we look for solutions

\[ u(\theta, \phi) = \sum_{j} \sum_{k} \hat{u}_{jk} v_{jk}(\theta, \phi). \]

A discrete Fourier approximation space with \(N\) basis functions is then

\[ V_F^N = \text{span} \{\exp(\imath k \theta)\,|\,\text{ for } k \in K\}, \]

where the index set \(K = \{-N/2, -N/2+1, \ldots, N/2-1\}\). For this demo we assume that the solution is complex, and as such there is no simplification possible for Hermitian symmetry.

The following approximation space is used for the \(\theta\)-direction

\[ \begin{equation} V^N = \text{span} \{\psi_j\}_{j=0}^{N-1}, \label{_auto4} \tag{5} \end{equation} \]

and the variational formulation of the problem reads: find \(u \in V^N \otimes V_F^N\) such that

\[ \begin{equation} \int_{\Omega} (-\nabla^2 u + \alpha u) v w d\sigma = \int_{\Omega} f v w d\sigma, \quad \forall \, v \in V^N \otimes V_F^N. \label{eq:u0} \tag{6} \end{equation} \]

Note that integration over the domain is done using spherical coordinates with an integral measure of \(d\sigma=\sin \theta d\theta d\phi\).

Implementation

A complete implementation is found in the file sphere_helmholtz.py. Here we give a brief explanation for the implementation. Start by importing all functionality from shenfun and sympy, where Sympy is required for handeling the spherical coordinates.

from shenfun import *
import sympy as sp

# Define spherical coordinates with unit radius
r = 1
theta, phi = sp.symbols('x,y', real=True, positive=True)
psi = (theta, phi)
rv = (r*sp.sin(theta)*sp.cos(phi), r*sp.sin(theta)*sp.sin(phi), r*sp.cos(theta))

Note that the position vector rv has three components (for \((x, y, z)\)) even though the computational domain is only 2D. Also note that Sympy symbols are both positive and real, and \(\theta\) is chosen to be along the first axis and \(\phi\) second. This has to agree with the next step, which is the creation of tensorproductspaces \(V^N \otimes V_F^N\).

N, M = 40, 30
L0 = FunctionSpace(N, 'C', domain=(0, np.pi))
F1 = FunctionSpace(M, 'F', dtype='D')
T = TensorProductSpace(comm, (L0, F1), coordinates=(psi, rv, sp.Q.positive(sp.sin(theta))))

Spherical coordinates are ensured by feeding coordinates=(psi, rv, sp.Q.positive(sp.sin(theta))) to TensorProductSpace, where the restriction sp.Q.positive(sp.sin(theta)) is there to help sympy. Operators like div(), grad() and curl() will now work on items of Function, TestFunction and TrialFunction using a spherical coordinate system.

To define the equation (6) we first declare these test- and trialfunctions, and then use code that is very similar to the mathematics.

alpha = 2
v = TestFunction(T)
u = TrialFunction(T)
mats = inner(v, -div(grad(u))+alpha*u)

Here mats will be a list containing several tensor product matrices in the form of TPMatrix. Since there is only one directions with non-diagonal matrices (\(\theta\)-direction) we can use the generic SolverGeneric1ND solver. Note that some of the non-diagonal matrices will be dense, which is a weakness of the current method. Also note that with Legendre one can use integration by parts instead

        mats = inner(grad(v), grad(u))
        mats += [inner(v, alpha*u)]

To solve the problem we also need to define the function \(f(\theta, r)\). To this end we use sympy and the method of manufactured solution to define a possible solution ue, and then compute f exactly using exact differentiation. We use the spherical harmonics function to define an analytical solution

alpha = 2
sph = sp.functions.special.spherical_harmonics.Ynm
ue = sph(6, 3, theta, phi)

# Compute the right hand side on the quadrature mesh
# That is, compute f = -div(grad(ue)) + alpha*ue
f = (-div(grad(u))+alpha*u).tosympy(basis=ue, psi=psi)
fj = Array(T, buffer=f)

# Take scalar product
f_hat = Function(T)
f_hat = inner(v, fj, output_array=f_hat)

u_hat = Function(T)
Sol = la.SolverGeneric1ND(mats)
u_hat = Sol(f_hat, u_hat)

Having found the solution in spectral space all that is left is to transform it back to real space.

uj = u_hat.backward()
uq = Array(T, buffer=ue)
print('Error =', np.linalg.norm(uj-uq))

Postprocessing

We can refine the solution to make it look better, and plot on the unit sphere using either mayavi or plotly using the shenfun function surf3D().

u_hat2 = u_hat.refine([N*2, M*2])
fig = surf3D(u_hat2.backward().real, wrapaxes=[1])
fig.show()