On this page

Parallel shear flows

The Navier-Stokes equations are nonlinear because of the convective term, \((\boldsymbol{u} \cdot \nabla)\boldsymbol{u}\), and in general not analytically solvable for most problems in fluid mechanics. The equations can be solved analytically when the convective term is zero and for a few other simplified flows. In chapter 3 of White we start by considering the types of flow where convection is zero.

The convection term is never negligible for turbulent flows, where the flow rapidly changes direction in a seemingly chaotic fashion. We will get back to turbulent flows in Chapter 6. For now we assume the flow is laminar. For a laminar flow the convection term will be zero for a parallel shear flow where the geometry is infinite in at least one direction and the velocity vector is parallel to the walls of the geometry. For example, a pipe flow or a plane channel flow as shown below

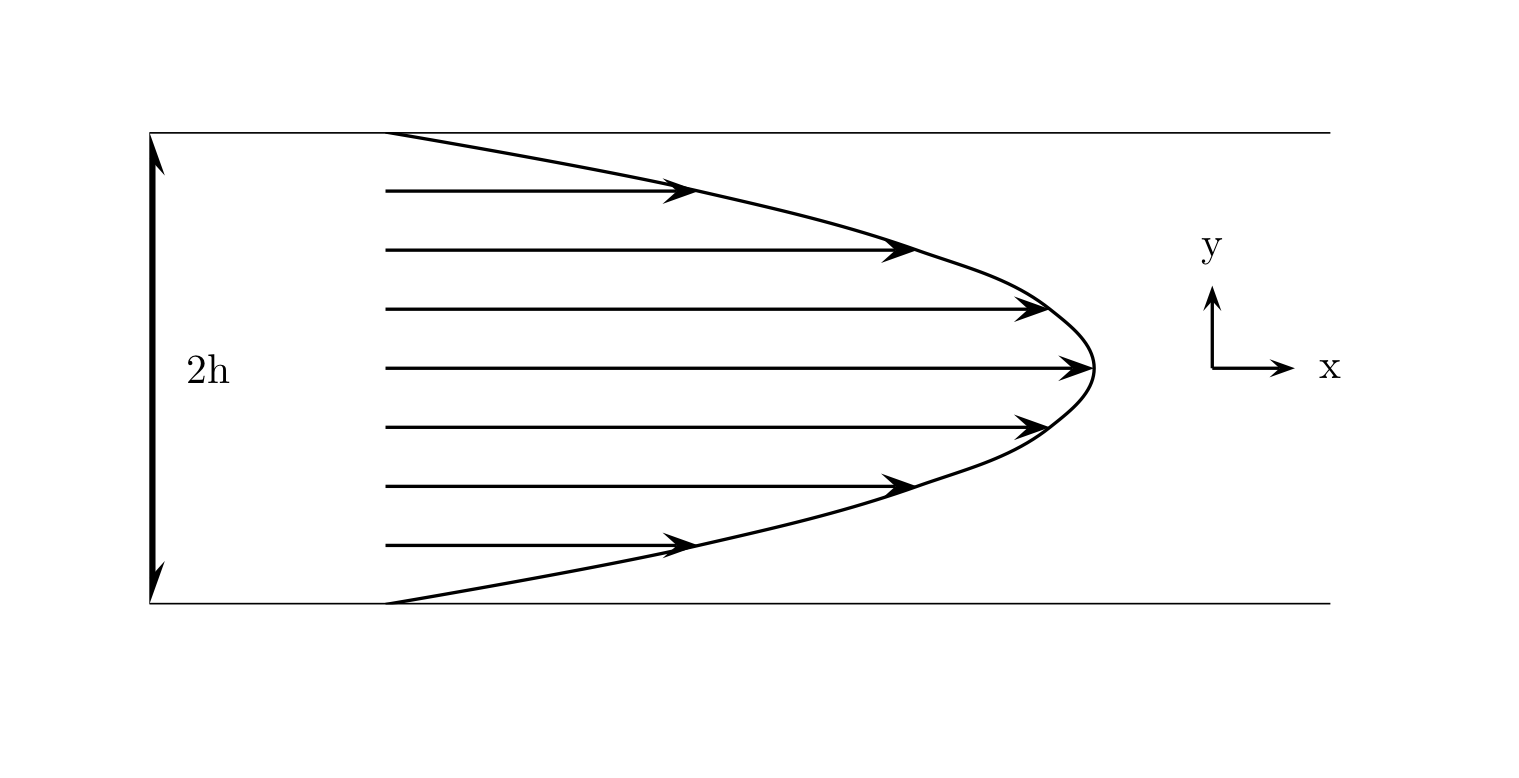
../../_images/channelprofile3.png

Fig. 1 Channel flow

where there is only one nonzero component of the velocity vector, and the velocity vector is parallel to the surrounding walls. The gradient of this velocity component is normal to the wall and as such \(\boldsymbol{u} \cdot \nabla u = 0\) and the Navier-Stokes equations reduce to the linear equations

\[\begin{split}\begin{aligned} \frac{\partial \boldsymbol{u}}{\partial t} &= -\frac{1}{\rho} \nabla p + \nu \nabla ^2 \boldsymbol{u} + \boldsymbol{f}, \\ \nabla \cdot \boldsymbol{u} &= 0. \end{aligned}\end{split}\]

Since the equations are linear it should not be surprising to find that there are many analytical solutions available for laminar parallel shear flows.

If the only nonzero velocity component is in the x-direction, then \(\boldsymbol{u}=(u, 0, 0)\) and the Navier-Stokes equations reduce to

\[\begin{split}\begin{aligned} \frac{\partial u}{\partial t} &= -\frac{1}{\rho} \frac{\partial p}{\partial x} + \nu \nabla ^2 u + f_x, \\ \frac{\partial u}{\partial x} &= 0. \end{aligned}\end{split}\]

which is also valid for the axial component of cylindrical coordinates (see Ch. 3-2.2). There are two types of parallel shear flows: Couette and Poiseuille. Couette flows are driven by moving walls. Friction, i.e., drag or viscous forces are then responsible for “dragging” the fluid with a direction aligned with the wall. For Poiseuille flows the driving force is a pressure gradient that can be generated using a pump.

Chapter 3 Couette flows